Stochastic Gradient Descent
경사하강법(Gradient Descent)을 사용해 10억개의 단어를 가진 말뭉치에 크기 5의 윈도우를 사용해서 word2vec 모델을 만든다고 하면, 10억개의 중심 언어와 100억개의 주변 언어를 가질 것이다. softmax를 100억번이 넘게 계산해야 기울기를 구할 수 있는데, 그래이디언트 계산에서 작은 부분을 차지하는 연산에 어마어마한 시간이 걸리므로 학습이 느리게 진행될 거다.
따라서 사람들은 모든 파라미터를 한 번에 다 업데이트하는 경사하강법 대신 윈도우를 반복적으로 샘플링하고 업데이트하는, mini-batch를 사용하는 확률적 경사하강법(Stochastic Gradient Descent, SGD)를 사용한다. 보통 32 혹은 64개의 작은 묶음으로 샘플링한 다음, 이 묶음 단위로 기울기를 계산한다. CPU나 GPU 메모리 구조 상 배치 사이즈는 2의 제곱수로 정하는 것이 좋다.
SGD를 사용할 때의 2가지의 장점이 있다.
- 기울기 계산에 하나의 데이터를 사용하는 것보다 많은 데이터에 대해 평균을 내서 계산했기 때문에 그래이디언트의 노이즈가 줄어든다.
- GPU를 통해 동일한 작업을 병렬 처리하여 계산 속도를 빠르게 할 수 있다.
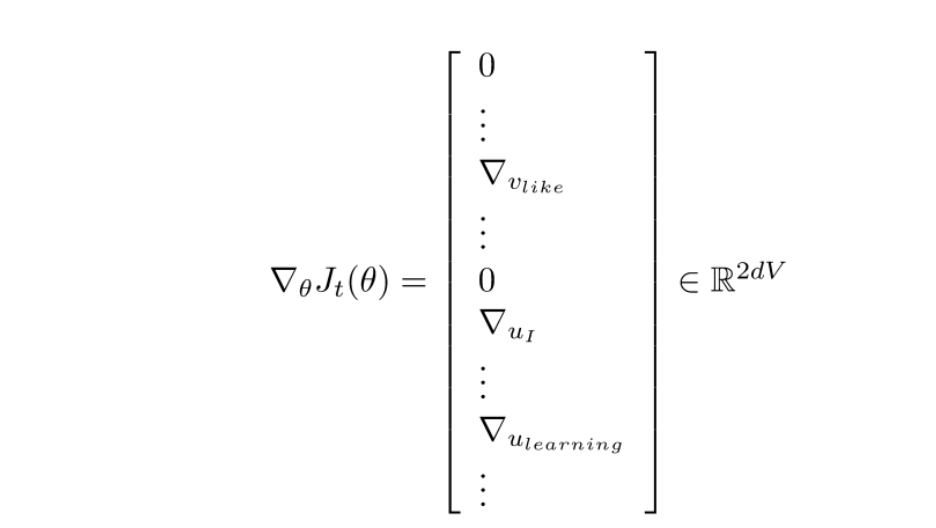
하지만 단점도 역시 존재한다. 각 윈도우마다 $2m + 1$개의 단어만 가지므로, $J_t(\theta)$에 대한 그래이디언트 벡터는 말뭉치의 모든 단어 중 윈도우에 포함된 $2m+1$개의 단어만 유의미한 값을 갖고 나머지는 0인 희소 벡터(sparse vector)가 될 것이다. 일부 단어를 학습하기 위해 역전파 과정에서 전혀 상관없는 단어들도 같이 업데이트를 하게 되는 불필요한 상황이 벌어지게 된다.
Word2vec의 2가지 모델
word2vec에는 2가지 모델이 있다. 중심 단어가 주어지면 주변 단어를 예측하는 Skip-grams(SG) 모델과, 주변 단어를 통해 중심 단어를 예측하는 Continuous Bag of Words(CBOW) 모델이다.
지금까지 살펴본 word2vec은 skip-gram 기반 모델이며, CBOW는 중심 단어를 예측하기 위해 Naive Bayes 모델처럼 주변 단어들의 확률 정보를 가지고 독립적으로 계산하는 방법이다.
Negative Sampling
SGD의 단점으로 '연관 없는 단어에 대한 불필요한 업데이트'를 말했었다. Negative Sampling은 전체 단어 집합이 아닌 연관이 있어 보이는 일부 단어 집합의 학습에 집중할 수 있도록 만드는 방법으로, SGD보다 계산량을 줄일 수 있다.
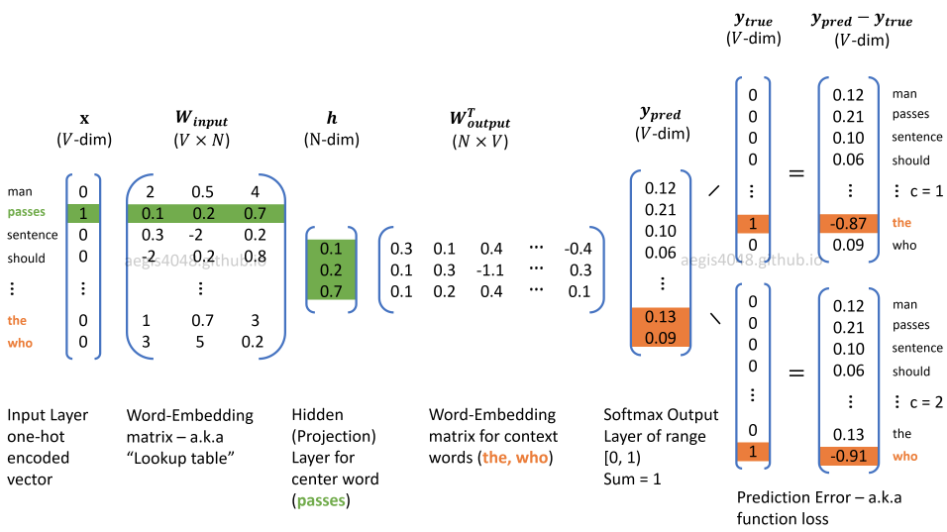
위 이미지는 기존 skip-gram의 작동 방식을 표현한 그림이다. 한 중심 단어에 대해 어떤 단어가 주변에 등장할 확률인 softmax output $y_{pred}$와 실제 주변 단어의 one-hot vector인 $y_{true}$와의 차이를 구해 error를 구하며, 이 과정에서 주변에 등장하지 않는 단어들과의 error를 구해 $y_{pred}$를 갱신하게 되므로 계산이 비효율적이게 되는 것이다.
$$P(o|c) = \cfrac{exp(u^T_ov_c)}{\sum_{w\in V}exp(u^T_wv_c)}$$
또 위의 식의 분모를 보면 중심 단어 벡터와 모든 단어 벡터에 대한 내적값을 계산해 더하는데, 이걸 계산하는 데 굉장히 오랜 시간이 걸릴 것이다.
이런 단점을 개선할 수 있는 방법으로 Negative Sampling이 있다. Negative Sampling은 기존 skip-gram이 풀던 문제인 다중 클래스 분류 문제를 이진 로지스틱 회귀 문제로 바꾼 것이다. 실제로 중심 단어 주변에서 관찰된 단어(=주변 단어)들은 1의 레이블을 주고, 주변에서 관찰되지 않은 단어(!= 주변 단어)들 중 몇 개를 랜덤으로 뽑아 0의 레이블을 주어 주변 단어와 그렇지 않은 단어를 구별해낼 수 있도록 학습하는 것이다. 이 방법의 이름이 Negative Sampling인 이유가 바로 레이블이 0(negative)인 단어들을 샘플링해서 주변 단어들과 함께 학습시키기 때문이다.
Negative Sampling에서 최소화해야 하는 목적 함수는 다음과 같다.
$$J_{neg-sample}(o, v_c, U) = -\log(\sigma(u_o^Tv_c))-\sum_{k=1}^K\log(\sigma(-u_k^Tv_c))$$
- 첫번째 항은 주변 단어와 중심 단어 사이(True pair)의 내적 + sigmoid + log -> 가능한 크게
- 두번째 항은 랜덤으로 선택된 $K$개(보통 $K$ = 10 ~ 15)의 단어와 중심 단어 사이(Noise pair)의 내적 + sigmoid + log -> 가능한 작게
주변 단어가 아닌 단어가 negative sample로 뽑힐 확률은 다음과 같다.
$$P(w_i)=\cfrac{f(w_i)^{3/4}}{\sum_{j=0}^nf(w_j)^{3/4}}$$
찾아보니 Negative Sampling 외에도 다른 방법이 있는 것 같다. Subsampling frequent words는 말뭉치에서 자주 등장하는 단어는 확률적으로 학습을 skip하는 방법이다. 등장 빈도만큼 업데이트 될 기회가 많기 때문이다. Subsampling frequent words에 관한 내용은 여기 참고.
Co-occurrence matrix와 차원 축소 방법
Co-occurrence matrix는 global co-occurrnece statics 정보를 저장하기 위해 고안된 단어 사이의 동반 출현 빈도수 정보를 담은 행렬이다. direct prediction 기법인 word2vec과는 다르게 count-based 기법이며, 중심 단어를 기준으로 움직이는 슬라이딩 윈도우 내에서의 빈도를 계산하는 Window based co-occurrence matrix와 한 문서를 기준으로 각 단어의 빈도수를 계산하는 Word-document matrix가 있다. window based의 경우 word2vec와 유사하며 단어간의 유사도를 찾기 수월하다. word-document의 경우 Latent Semantic Analysis(LSA)로 넘어가게 되며, 문서의 전반적인 주제를 찾기 수월하다.
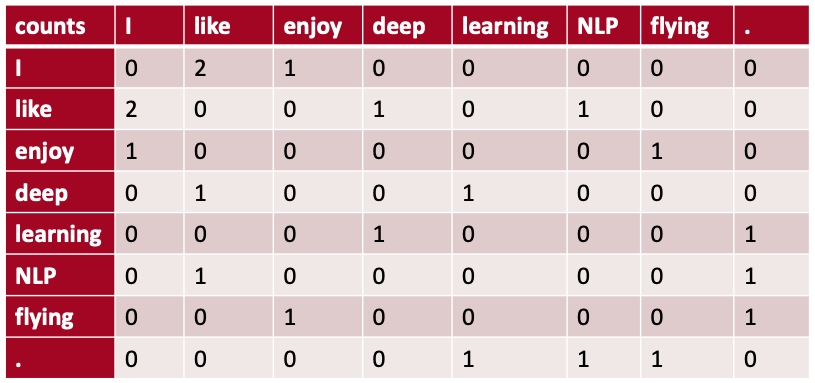
window-based co-occurrence matrix의 예시로, 말뭉치에 아래의 3개의 문장이 있다고 생각해 보자.
- I like deep learning.
- I like NLP.
- I enjoy flying.
이 문장을 가지고 window based co-occurrence matrix를 만든 결과는 아래와 같다. 비슷하다고 생각되는 두 단어는 이 co-occurrence matrix에서 유사한 vector(행) 값을 가질 거라고 예측할 수 있다.
하지만 이 co-occurrence matrix 역시 0이 대부분인 희소 행렬이고, 단어의 개수가 증가할수록 차원이 폭발적으로 증가한다. 그래서 보통 SVD(Singular Value Decomposition)나 LSA 등의 방법을 통해 차원을 축소해서 사용한다. SVD, PCA, LSA와 관련된 내용은 ratsgo님의 블로그 글을 참고하자.
Scaling the counts
각 단어에 대한 카운트를 조정하는 것은 학습에 크게 도움이 된다.
- 자주 등장하는 단어들(ex. the, he, has)은 다른 단어들보다 더 큰 임팩트를 가지게 되는데, 일정 카운트 이상 등장하는 단어들은 모두 무시하는 등의 방법으로 조정해준다.
- 또, 같은 윈도우 안의 주변 단어라고 해도 중심 단어와 더 가까운 단어와 덜 가까운 단어 사이의 중요도를 차등으로 주는 방법이 있다.
- 다른 방법으로는 단순 집계 대신 피어슨 상관관계를 사용하고, 음수 값은 0으로 설정하는 방법이 있다.
GloVe(Global Vectors for Word Representation)
참고
https://wikidocs.net/22885
https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/09/glove/
GloVe는 count-based의 LSA, directed prediction based의 word2vec의 단점을 보완하기 위해 등장한 단어 임베딩 방법론이다. LSA로는 단어 간의 관계를 파악하기 어려우며, 빈도수가 높은 단어에 과도하게 높은 중요도를 부여한다. 그리고 word2vec은 단어 간의 유사성 그 이상의 패턴을 파악할 수 있지만 빈도수와 같은 통계 정보를 효율적으로 사용할 수 없다. GloVe는 목적함수를 임베딩된 두 단어 벡터의 내적이 말뭉치에서 동시에 등장할 확률의 로그값이 되도록 정의하여, word2vec의 장점인 단어 벡터 간 유사성 파악과 LSA의 장점인 통계 정보 이용을 모두 갖게 했다.
GloVe의 학습 방법을 살펴보자. 아래의 표는 전체 학습 말뭉치 중 두 단어가 동시에 등장한 빈도를 각각 센 다음 전체 말뭉치의 단어 개수로 나눈 동시 등장 확률을 나타낸 표다. 예를 들어, 전체 말뭉치에서 'ice'와 'solid'가 동시에 등장할 확률은 0.00019다. 'steam'이 등장했을 때 'solid'도 동시에 등장할 확률은 0.00019보다 훨씬 낮은 0.000022다. 'ice'가 'steam'보다 'solid'와 더 연관성이 높으므로 당연한 결과다. 그러므로 $\cfrac{P(solid|ice)}{P(solid|steam)}$은 1보다 훨씬 큰 8.9를 갖는다. 이것과는 반대로 x가 water나 fashion일 때처럼 두 단어 벡터 모두 관련성이 높거나 별로 없는 경우는 1에 가까운 값이 나온다.
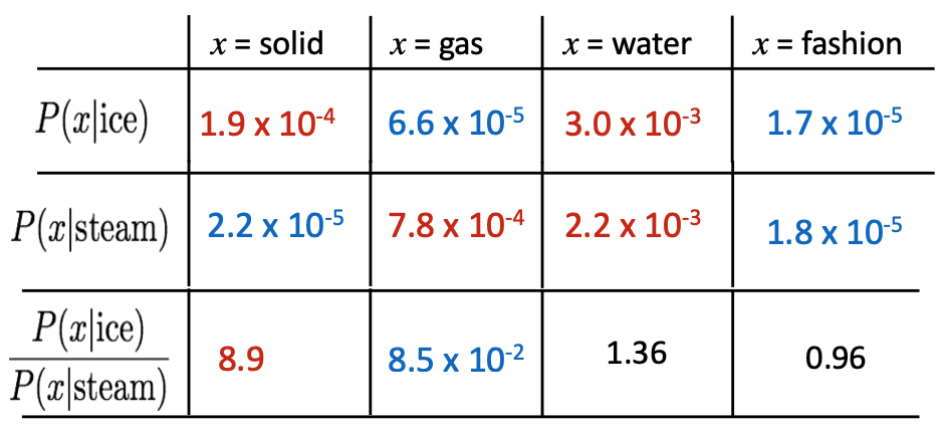
여기서 계산된 동시 등장 확률의 비율의 로그값이 단어 벡터들의 내적값과 같아지게 정의하면 두 단어 벡터간의 차이를 Linear한 형태로 표현할 수 있다. ($w_i\cdot w_j=\log P(i|j)$ 👉🏻 $w_x\cdot (w_a-w_b)=\log \cfrac{P(x|a)}{P(x|b)}$)
위의 아이디어에 따라 목적 함수는 아래와 같은 형태를 갖는다.
$$J = \sum_{i, j = 1}^{V}(w_i^T\tilde{w}n+b_m+\tilde{b}_n-\log{X{mn}})^2$$
여기서 $X$는 동시 등장 행렬로, 희소 행렬일 가능성이 높다. 동시 등장 행렬에서 동시 등장 빈도의 값 $X_{ik}$의 값이 굉장히 낮은 경우에는 거의 도움이 되지 않는다. 그래서 $X_{ik}$값에 영향을 받는 가중치 함수 $f(X_{ik})$를 목적 함수 $J$에 도입하게 된다.
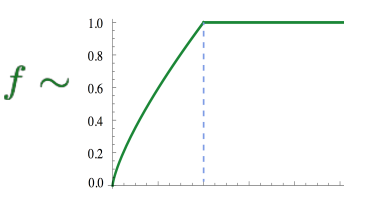
$f(X_{ik})$는 빈도수가 과도하게 높은 단어(a, it, is, the 등의 불용어)의 동시 등장 빈도수가 지나친 가중을 받지 않도록 함수의 최대값을 정해놓았다.
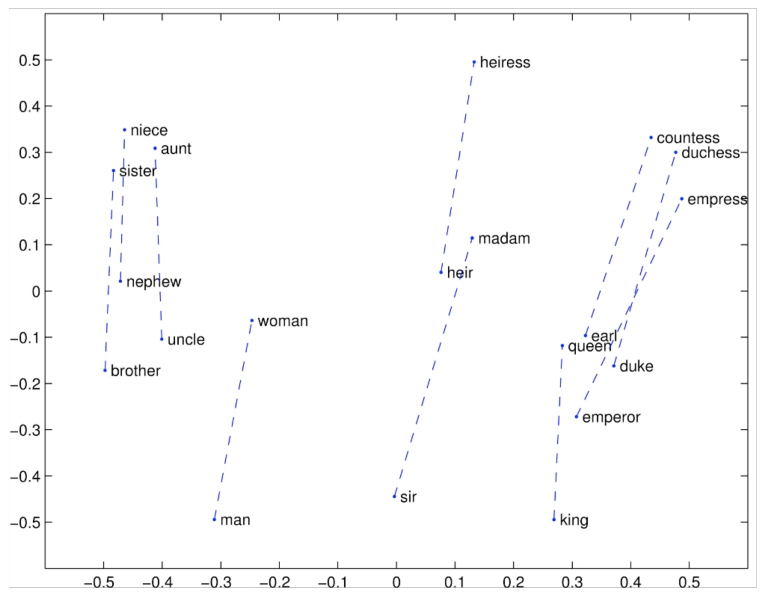
GloVe 모델을 사용하면 아래처럼 유사한 관계에 있는 단어들끼리 비슷한 Linear Property를 갖게 된다.
'Machine Learning > NLP' 카테고리의 다른 글
| [NLP] Transformer 알아보기 - (1) Encoder (0) | 2022.01.11 |
|---|---|
| Stanford CS224N (Winter 2019) | Lecture 1: Introduction and Word Vectors (2) | 2021.12.01 |
| [파이토치로 배우는 자연어처리] 레스토랑 리뷰 감성 분류하기 - (3) 감성 분류 모델 만들기 (2) | 2021.10.28 |
| [파이토치로 배우는 자연어처리] 레스토랑 리뷰 감성 분류하기 - (2) 문장 토큰화와 Dataset (0) | 2021.10.25 |
| [파이토치로 배우는 자연어처리] 레스토랑 리뷰 감성 분류하기 - (1)데이터 전처리 (0) | 2021.10.22 |
